Business — Banking — Management — Marketing & Sales

The limit distribution results from conditioning by one random factor the distribution of asset values within a portfolio. With full Monte Carlo simulations, we need to draw a large number of asset values for each firm consistent with the correlation structure of asset values. Chapter 48 illustrates the technique. We use here the same framework, but constrain the problem to a uniform correlation between all asset values.

CREDITRISK+

CreditRisk+ is a default model that generates loss distributions based on default events, recovery rates and exposure at book value. It is not a full valuation model, since exposure value does not change according to risk.

Major Features

CreditRisk+ utilizes an analytical framework, which makes it easy to manipulate and use numerical calculation algorithms to avoid full-blown Monte Carlo simulations. The next paragraphs summarize the major features of the model.

The mixed Poisson distribution plays a pivotal role in generating independent default events. The Poisson distribution tabulates the frequency of observing k defaults when the default intensity, or the number of defaults per unit time, has a fixed value n.Thisdefault intensity is the Poisson parameter. It is analogous to the default probability, except that it is a number of defaults.

The model necessitates dividing the portfolio into segments by risk class and exposure net of recoveries. This allows us to bypass the limitations of the Poisson distribution that generates the distribution of the number of defaults, without considering size discrepancies. This makes it necessary to control both size of exposure, net of recoveries, and default risk before, and model loss within, each band size. In practice, CreditRisk+ requires dividing the portfolio into segments by risk class and loss under default bands.

The mixed Poisson distribution uses a mixing variable q that allows the default intensity to vary according to whatever factors are relevant, or to run scenarios of default intensity. This provides the facility to model the default intensity as a function of economic factors.

In the special case where the mixing variable follows a gamma distribution, the resulting mixed Poisson is the negative binomial distribution. Under independence, this completes the analytical modelling of the loss distribution. The purpose of this extension is to allow default rates to vary and to fit the variation to the actual default rate volatility by adjusting accordingly the parameters of the gamma distribution.

The time intensity parameter makes defaults dependent on time, which is a useful feature for modelling the time to default. When aggregating distributions over all segments, it is possible to identify the time profile of default losses. Hence, the same framework provides a loss distribution at a preset horizon and also provides insights into time to default by segment.

Finally, the extended version of the model makes the mixing variable q dependent on a common set of factors to mimic correlations across portfolio segment distributions. To extend the model to correlation, CreditRisk+ makes the mixing variable a linear combination of external factors, such as economic conditions, with specific sensitivities. In order to proceed with this extension, CreditRisk+ uses specific properties of the mixed Poisson distribution. One property is that, when individual mixed Poisson distributions are independent, or if they depend on each other through the mixing variables only, the sum of the mixed Poisson distributions remains a mixed Poisson distribution. In addition, the mixing variable is a simple linear function of individual Poisson parameters and mixing variables (Chapter 47 further details these properties). Since CreditRisk+ makes only the mixing variable dependent on external factors, it complies with this condition. This common dependence across segments of the mixing variable on the same factors correlates the default rates. In addition, CreditRisk+ includes specific risk as an uncertainty generated by a factor independent of others. Since interdependency is user-defined, the model does not provide ways to define factors, sensitivities and the magnitude of specific risk. It simply provides an open framework to include these. By contrast, KMV Portfolio Manager is self-contained.

An attractive property is that loss distributions are entirely analytically tractable with adequate assumptions. CreditRisk+ also uses classical numerical algorithms applying to such actuarial distributions to speed up the calculation process.

The subsequent sections discuss these topics further: details of the Poisson distribution, properties of the mixed Poisson distribution, the correlation issue.

The Poisson Distribution

The Poisson distribution is widely used in insurance modelling. It provides the distribution of the number of defaults when defaults are independent. It models a number of defaults, ignoring size discrepancies of losses under default. Hence, it applies to segments, each of them being of uniform size and uniform default probability. CreditRisk+, like Credit Portfolio View (CPV), models default rates, not individual default probabilities. The density function of the Poisson distribution is:

where:

• n is the default intensity per unit time, for instance 1 year, or the average number of defaults in a 1-year period. It is also the Poisson parameter.

• k is the random number of defaults, from 0 to the maximum number of exposures in a portfolio segment.

• k! is the factorial of k.

If the number of yearly defaults is 3 out of 100 exposures, this corresponds to a yearly default intensity of 3% and a Poisson parameter equal to 3 per year. The probability of observing 8 defaults is:

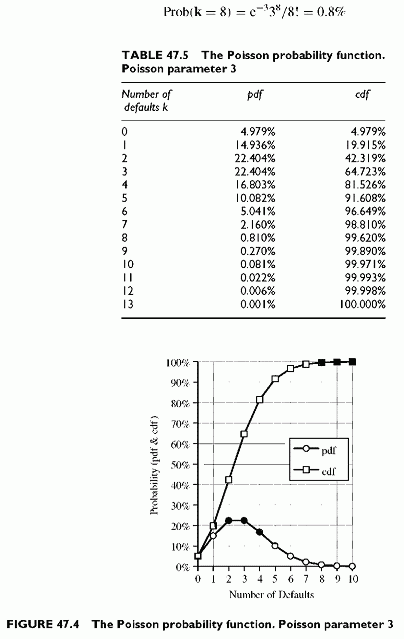
The mean of a Poisson distribution is the Poisson parameter, 3 in this case, and its volatility is its square root, or V3 = 1.732. Table 47.5 shows the probabilities of the various numbers of defaults with a mean of 3 defaults per year, and Figure 47.4 charts the probability density and the cumulative density functions.

The loss percentile corresponding to 99% is around 7 defaults. Converting the loss percentile into loss is straightforward with equal unit sizes. For instance, a $1000 unit loss would result in a $7000 loss percentile at the 1% confidence level.

To develop its analytical framework, CreditRisk+ uses probability generating functions¹ applying to independent events:

To combine all subportfolios, CreditRisk+ uses the fact that the sum of Poisson distributions is also Poisson distributed, with a Poisson parameter equal to the summation of all individual Poisson parameters.

The Mixed Poisson Distribution

The mixed Poisson distribution conditions the Poisson parameter with a random mixing variable  q. The Poisson parameter becomes nq, instead of the original n. The mixing variable q can be a simple scaling factor, but it is in general random. This allows the default intensity to fluctuate randomly. To make the analytics simple, it is necessary that E(q) = 1. When q> 1, the default intensity increases above the average, and conversely when q< 1.

The mixed Poisson has a number of desirable characteristics. The mean of the new distribution becomes E(q) x E(k) = n,where k is the random number of defaults, identical to that of the underlying Poisson distribution. In other words, average default intensity over all q values remains equal to the long-term average n. The scaling convention implies that E(qk) = n, as with the unconditional distribution. The variance of the number of defaults k becomes a(k)² = n + n²a(q)². It is larger than the Poisson variance n due to conditioning by a random variable. The conditioning makes the volatility larger, and the fat tail of the distribution longer than in the simple Poisson distribution.

The mixed Poisson distribution accommodates economic cycle effects, or using a discrete number of scenarios with subjective probabilities assigned to each of them. When allowing the intensity of default to be random, it is necessary to fit the mixing variable to the actual fluctuations observed. This is feasible directly when historical observations are available. However, this is more the case with insurance claims, for which there is plenty of data, than with credit data.

CreditRisk+ uses the attractive properties of the summation of mixed Poisson distributions to obtain the entire portfolio loss distribution. The sum is also a mixed Poisson, if the individual mixed Poisson distributions are independent, or if they depend on each other through the mixing variables only. The sum of the two distributions follows a mixed Poisson with a mixing variable q equal to the weighted average of the individual mixed Poisson variables q_x and q₂, the weights being the ratios of Poisson parameters n₁ and n₂ of the individual distributions to their sum:

This allows modelling of the entire aggregated loss distribution over the entire portfolio and opens the door to interdependencies between individual distributions as long as only the mixing variables embed them.

The smaller h, the larger the standard deviation of k, which corresponds to a larger volatility of Gamma(h, h), the distribution of q. In addition, simple algorithms allow us to calculate the distribution.

The final result is that the mixed Poisson models the default distribution of each portfolio segment, including fluctuations of the default intensity. The distribution has an analytical form as long as we stick to the negative binomial case, implying the usage of a standardized gamma distribution for the conditioning variable q. The standardized gamma distributions per segment serve for modelling cyclical fluctuations of q.

Aggregating the distributions across portfolio segments requires convolution of the distributions, which is a simple technique applying to independent distributions. Convolution simply says that the joint probability of any number of defaults in one segment and another number in a second segment is the product of the probabilities of having these numbers of defaults.

Correlating Segment Loss Distributions

The CreditRisk+ technique for correlating losses across segments consists of making the mixing variable of individual distributions dependent on a set of common factors. The resulting mixed Poisson has a mixing variable that is a simple linear function of segment-specific mixing variables. Since the conditioning on factors is deterministic, there is no specific risk independent of factors. To correct this, CreditRisk+ adds one sector, which generates a specific random noise. Portfolio segments are not sensitive to this particular factor, so it does add specific risk as an additional segment whose risk is unrelated to others.

Loss Distributions: Monte Carlo Simulations

This chapter explains and illustrates the Monte Carlo simulation methodology with two approaches: the option theoretic approach using Monte Carlo simulations of asset values and the econometric modelling of Credit Portfolio View (CPV). In both cases, generating portfolio value distributions requires generating risk drivers complying with a given correlation structure. Both sample simulations use a single-factor model to generate a uniform correlation between the firms of the portfolio.

Asset value simulations use a single-factor model of asset values, with a random specific error term, uniform correlation between assets, uniform sizes of exposures, under default mode only. The asset values are a linear function of a common factor, representing the state of the economy, and of an error term, independent of the state of the economy, representing specific risk. Monte Carlo simulations generate random sets of future values of the economic factor and of the specific risk, from which the asset values derive directly. This is a much more restrictive framework than actual portfolio models. However, it illustrates the essential mechanisms of the process. Moreover, the same technique allows us to vary the default probabilities and the sizes of exposures across exposures, and to use any variance-covariance structure. The examples in Chapters 55 and 56 use the same single-factor model of asset values with differentiated exposures and default probabilities. At this stage, the purpose is only to illustrate the essentials of the technique and the sensitivity of portfolio value distributions to the uniform correlation.

The example shows that the multiple of the loss volatility when moving from independent default to a 30% asset correlation is above 2.5, with a portfolio of uniform default probability equal to 1%. The loss percentile at the 99% confidence level, when moving from independent default to a 30% asset correlation, increases by a scale factor of around 2.5. This illustrates the importance of correlation when looking at extreme losses of portfolios.

For a simplified implementation of simulation under the econometric framework of CPV, the same basic principles apply. A single-factor model drives an economic index directly related to the default rates of two portfolio segments through logit functions. The economic index is a linear function of an economic factor, representing the state of the economy and of an error term, representing specific risk. Monte Carlo simulations generate random sets of future values of the economic factor and of the specific risk, from which the economic index derives. Once the economic index is converted into default rates through logit functions, we obtain correlated distributions of the default rates of two portfolio segments. A large number of trials provides the full distributions of the default rate values of the portfolio segments and of their sum over the entire portfolio. The example does not intend to replicate the CPV framework, but provides a simple illustration.

The first section summarizes the main features of KMV Portfolio Manager and specifies the simplified framework used here to conduct the sample simulations based on random asset values of obligors. The second section provides simple simulations inspired by the CPV approach. The first subsection details the structure of CPV. The second subsection specifies the simplified assumptions used to generate the distributions of segment default rates and of the overall portfolio.