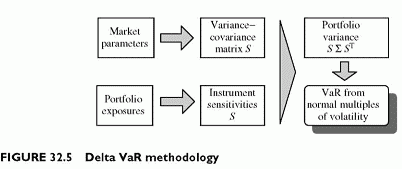
EXTENSIONS OF THE DELTA VAR METHODOLOGY
Category: Risk Management in Banking
There are several extensions of this basic analytical model. E-VaR is the expectation of VaR conditional on exceeding the threshold at the preset confidence level. It is easy to derive under the normal assumptions. Delta-Gamma VaR relies on shortcuts to capture
VaR (1%) – 2.33×121=291
non-linearities. When moving along this path, we soon encounter complexities that lead to the multiple simulation techniques.
E-VaR
E-VaR is the expected value conditional on exceeding a percentile. This is the average size of the loss conditional on exceeding the percentile. With a loss L in absolute value:
Prob (L>L(a))=Ф(a)
The probability Prob(L = L) that the random loss L takes the value L conditional on exceeding L(a) is the unconditional probability that the loss has the value L exceeding L(a) divided by the unconditional probability that the loss exceeds L(a), or $(a):
Prob (L>L(L>L(a)))=pdf(L)/Ф(a)
The expectation of the loss given that the loss exceeds the upper bound is the cumulative density function of L, or Prob[L = L|L >L(a)] = [j»^a) L x pdf(L)]/$(a).This formula requires the calculation of the expectation of a truncated distribution, truncation occurring at L(a). There is a general formula of the expectation for random normal variables. The formula collapses to a simple one when using a normal standardized variable (mean 0 and variance 1) truncated at the lower end by L(a):
E(L(L>L(a)))=+pdf(a)/Ф(a)
Delta-Gamma VaR
A more important variation addresses the convexity issue for options that makes the linear approximation collapse. Because of convexity, sensitivity varies with the underlying parameter. Even with short periods, such variations are not negligible. A proxy of this variation is the Gamma sensitivity. The Gamma is the derivative of Delta with respect to the underlying of an option.
It is therefore possible to extend the Delta VaR to the Delta-Gamma VaR using the Gamma terms. The mathematical formula is the Taylor expansion of the VaR up to the second order7, while the Delta VaR uses only the first order. The formula is similar to the general Delta VaR formula, except that the sensitivity with respect to the underlying of options includes the Delta and the Gamma terms in a linear fashion. Hence, the concept is similar, while using Gamma as a linear proxy for the Delta variation. It is possible to implement a semi-full simulation using the sensitivities to each factor, as linear functions of these factors (delta, gamma, rho, theta) and to recalculate the values. The same technique allows us to decompose the price of derivatives with respect to the Greeks—delta, gamma, nu and rho—as sensitivities of the derivative value with respect to these parameters. These formulas apply to any interest rate security. For an option, we substitute the corresponding Greeks in the coefficients:
For an interest rate asset, the formulas providing the value variation of an option under the Delta and the Delta-Gamma variations are:
Unfortunately, the function is not linear any more8. The Cornish-Fisher expansion provides a relationship between the moments of a distribution and its percentiles9.
Moving to Multiple Simulations and Full Revaluations
When the final distribution of the portfolio value is not normal, we cannot rely only on the analytical calculation allowed by normal distributions. The process is similar. Instead of using correlations between market parameter values, we correlate the random terms in the processes mimicking the time paths of market parameters. Asset value changes follow correlated lognormal distributions.