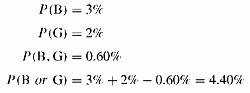Business — Banking — Management — Marketing & Sales

Support is not identical to third-party protection because it can be negative. A positive support is similar to a guarantee. The value of support depends on the joint default probability of the borrower and the supporting entity. The negative support case necessitates a specific analysis:

• Under negative support, the supporting entitys default triggers the default of the borrower.

• Under dependency of the supporting entity on the borrowers default, the borrowers default triggers the supporting entitys default.

These are extreme cases, since such relations are not deterministic. Support changes in the conditional default probability given either the default of the supporting entity or the default of the borrower. For simplification, we consider only the extreme deterministic relationships. With negative support, the risk is more an either/or risk: either the borrowers default or the insurers default triggers a default event for the lender.

Either/or events follow different rules from and rules for combining default probabilities. The probability that either B or G defaults is the sum of their default probabilities minus the probability that both occur. The general corresponding formula is:

P(borrower defaults or supporting entity defaults) = P(borrower defaults) + P(supporting entity defaults) — JDP(both default)

The correlation still influences the risk through the joint default probability. The formula is consistent with the intuition that the lenders face both risks since the joint default probability is generally small, unless correlation is high. Therefore, the default event probability becomes approximately equal to the sum of the standalone probabilities of the borrower and the guarantor. The following calculations consider that the default probabilities are:

The default probability under support is much higher than any one of the standalone default probabilities. The gain is negative, consistent with a negative support.

The usage of the above relationship is subtle. In fact, if we consider that a single default, either that of B or of G, deterministically triggers the default of the other, the correlation is 1. If the correlation is 1, consistency constraints imply that both default probabilities are equal and that their values are equal to the joint default probability. When either B or G triggers the default of the other, it becomes impossible that the standalone probabilities differ from each other. This is a limit case. In practice, the relationship is not necessarily symmetrical. It is possible that the supporting entity default triggers that of the borrower while the reverse is not true. The correlation coefficient does not reflect this asymmetry of causalities.