Business — Banking — Management — Marketing & Sales

Credit Risk Time Profiles

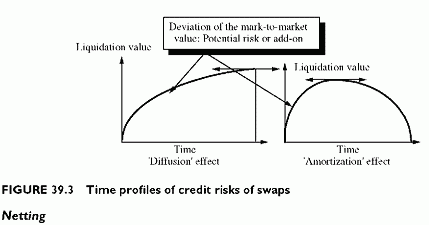
The time profiles of add-ons for swaps have different shapes. When the last flows are the most important, the risk usually increases with time because of the effect of increased volatility of this last flow. This is the usual profile of currency swaps. When amortizing effects are important, the number of flows decreases with time. Simultaneously, the volatility of market parameters increases with time. These two factors have offsetting effects on the deviations of the liquidation value. When amortization is negligible, the increase in volatility results in increased deviations of liquidation value with time. When the amortization effect dominates, the liquidation values obtained from the bounds of market parameters decline. Hence, there is a maximum for the deviations of the liquidation value of the swap somewhere between now and maturity. Potential risk usually peaks between 1/3 and 1/2 of the residual life (Figure 39.3).

Credit Risk Exposure for Portfolios of Derivatives

With derivative portfolios, the total liquidation value is the sum of individual liquidation values. With netting agreements, positive deviations net against negative deviations. In addition, individual deviations depend on each other, since they are market-driven and market parameter variations comply with a correlation structure.

With netting agreements, banks exchange only the netted value of instruments. For instance, if A has two transactions with B whose liquidation values are 50 and —20, the risk exposure is the netted value, or +30. This is because only netted flows count. Without netting agreement, only positive liquidation values are at risk. In the above example, the risk will be +50 and 0 for the second transaction. The exposures are added according to the rule of positive liquidation values. Since netting agreements reduce the risk exposure, adding individual forfeit measures of credit risk is not adequate. The liquidation value of the portfolio at any future date should net the liquidation values of individual instruments. This requires direct measures of the current and potential risks for the entire subportfolio subject to netting.

Portfolio Exposure and Correlation between Market Parameters

The evaluation of offsetting effects within portfolios is not simple because the individual instrument deviations do not add. Summing individual risks would mean that all instruments reach their upper bound values at the same time. This is an unrealistic assumption since the different instruments depend on different market parameters that cannot deviate simultaneously in the most adverse direction.

The interdependency between market parameters is a necessary input for defining the upper bound of the portfolio value. Interest rates in one currency correlate, exchange rates correlate with interest rate differentials across currencies, and so on. The issue is to determine the upper bound of the mark-to-market value of the portfolio given such correlations.

The adequate methodology relies on correlations between market parameters or on full simulations. The methodology is the same as that used to value the VaR for market risk for portfolios. The correlation methodology determines the volatility of the mark-to-market value of the portfolio given market parameters, their interdependencies and the sensitivities of the instruments of the portfolio to the different market parameters. Note that sensitivities change at different time points because of the amortization of cash flows. In addition, they change over long periods because they are local measures.

The simulation methodology (Monte Carlo) tests all possible values using sets of market parameter values consistent with their interdependencies. Both the generation of random values constrained by the correlation structure and historical sets of observed values work.

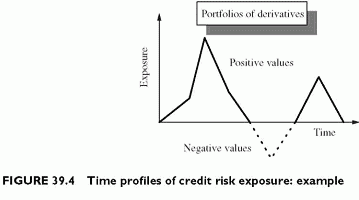
The multiple simulation technique is capable of handling options. The technique generates a distribution of the possible values of the portfolio for each future date. The upper bound at a given confidence level results from this distribution. The composition of the portfolio changes over time. Some derivatives reach maturity and their liquidation value vanishes at that time. Therefore, the time profile of exposures has no typical shape because the portfolio amortization combined with netting effects generates any shape for the time profile (Figure 39.4).

A final remark is that credit risk looks for positive variations of market values, whereas market risk cares for negative variations. Hence, there is a case for netting the market risk and the credit risk of derivatives. However, this is both complex and not necessarily relevant. The short-term horizon of market risk does not compare, in terms of deviations of values, with the long-term horizon of derivatives. The small adjustment might not be worth the effort. In addition, it is conservative to add both risks, rather than net them.

From Guarantees to Structures

Collaterals, loan contracts and covenants serve to control the borrowers risk-taking propensity and increase recoveries under default. Structures are Special Purpose Vehicles (SPVs) that have no credit standing by themselves: they offer credit risk protection from collateral and from covenants ruling the life of the SPV, which customizes both default probabilities and recoveries according to the seniority level of lenders.

The regulators recognized the risk mitigating effects of various forms of guarantees received in the foundation approach of the New Basel Accord of 2001. Recoveries reduce loss under default and if their value is reasonably certain, they reduce the capital charge. Losses for credit risk depend directly on recovery rates, making these key inputs for measuring credit risk. The New Accord provides strong incentives for building up data on recoveries. Recoveries depend on the nature of protection, making it necessary to differentiate them according to the nature of guarantees.

Collaterals are assets seized by lenders in the event of default.

Third-party guarantees are contractual obligations of a guarantor to act as a substitute for the primary borrower if he defaults on his payment obligations. A third-party guarantee is a legal obligation. Support, from the head of a group to a subsidiary, is informal. It designates the supportive behaviour of holding companies towards subsidiaries whose credit standing deteriorates up to default. Support is like third-party guarantees except that there is no binding legal agreement.

Credit derivatives are similar to guarantees and insurances, but they are distinct contracts from loans and relate to underlying assets that are not necessarily those of lenders. Sellers of credit derivatives are sellers of a protection, or insurers, buyers of credit derivatives are buyers of protection.

Whenever there is an exposure to the risk of a pair of obligors, through guarantees or credit derivatives, default occurs when both obligors default. This is a double, or joint, default event of the primary borrower and the guarantor. Its probability depends on how interdependent their risks are.

Covenants are contractual clauses, imposed on borrowers, the breach of which triggers a prompt repayment of outstanding debt. Covenant breaches require waivers from lenders, implying renegotiation, to continue operations.

Structures are the ultimate stage of protection shield for lenders. The SPV protects lenders with covenants ruling the structures behaviour, allowing for early default events before potential losses of lenders get too high and corrective actions triggered by breaches of covenants.

This chapter describes the various credit risk mitigants and serves as an introduction to valuation, when feasible, addressed in the next chapter. The sections address sequentially collateral, third-party guarantees, covenants and structures with SPVs.