Business — Banking — Management — Marketing & Sales

The standard representation of the diversification effect applies to portfolio and asset returns. The principles date from Markowitz principles (see Markowitz, 1952). The portfolio return varies with common factors and because of specific risk, the risk independent of common factors. Extending the number of assets creates diversification because the specific risks of individual asset returns offset each other. The undiversifiable risk is the general risk common to all assets. This well-known result applies notably to stock returns and is the basis for diversification.

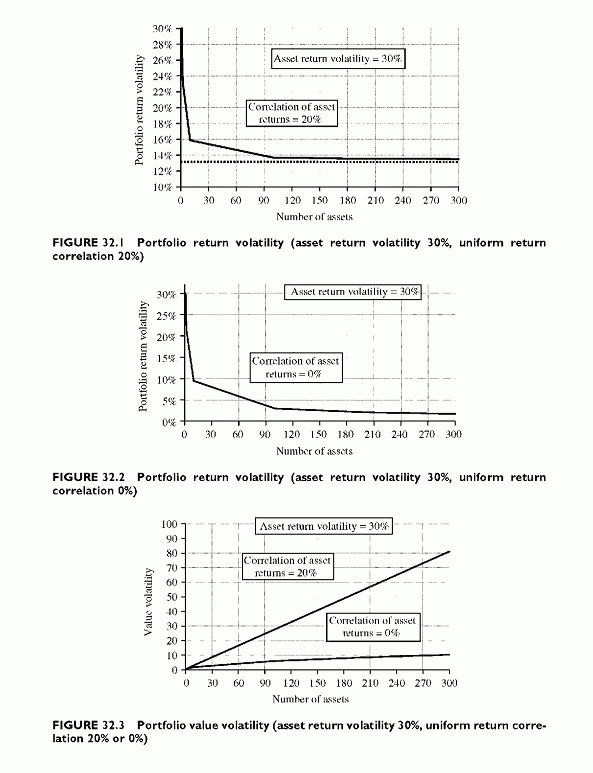
When looking at market risk, the focus is more on values than on returns. The diversification reduces the market risk because it reduces the volatility of the market value of the portfolio. When looking at values rather than returns, the same basic mechanisms of diversification apply. Nevertheless, unlike return volatility that declines to a floor corresponding to general risk, the volatility of the value increases with each new asset. The increase in value volatility of the portfolio increases with the portfolio average return correlation. Figures 32.1 and 32.2 show the variation of the portfolio return volatility and of the portfolio value volatility with average correlations of asset returns set to 20% and 0%, respectively. The figures show that the portfolio value volatility varies with the number of assets in both cases of independence and correlated returns (Figure 32.3).

The appendix to this chapter summarizes the calculations of the volatility of the portfolio return and the portfolio value for the simpler case of a portfolio with uniform asset return volatility, asset return correlation and uniform exposure. For a uniform exposure—asset return volatility—asset return correlation, when N gets large, the portfolio value volatility is proportional to the number of assets N. The coefficient is N xV₀ x a x ^fp, where Vq, a and ^fp are the uniform unit asset value, the uniform asset return volatility and the uniform asset return correlation. When adding one exposure, the additional volatility is simply V₀ x a x ^fp, and it becomes constant when N is large enough. The volatility is much higher than the volatility under independence, which grows as the square root of N when N becomes large enough.

Most popular kitchen countertops quartz kitchen countertops.